AICS实现对积分过程的稳定控制

背景介绍

积分环节是流程行业生产中常见的动态过程。积分环节过程的特点是，当过程的所有MV为常数时，过程的CV不会到达一个稳态值，而是会线性增加或者减少，积分环节过程是一个不稳定的过程。因此，设计一个合理的控制器稳定控制积分环节过程就显得尤其重要。工业场景中大多数容器的动态过程都是积分过程，比如水箱、储料仓等。

控制器搭建

在AICS画布中拖入DT-MPC组件，将MV和CV的数据接入相应入参端口。与非积分环节的控制器配置相比，积分环节的控制器配置主要有两点不同。

• MPC模型配置

在配置具有积分环节性质的CV的模型时，只需配置该积分环节的差分阶跃响应模型即可。例如在此案例中，MV和CV之间的阶跃响应模型为下图。

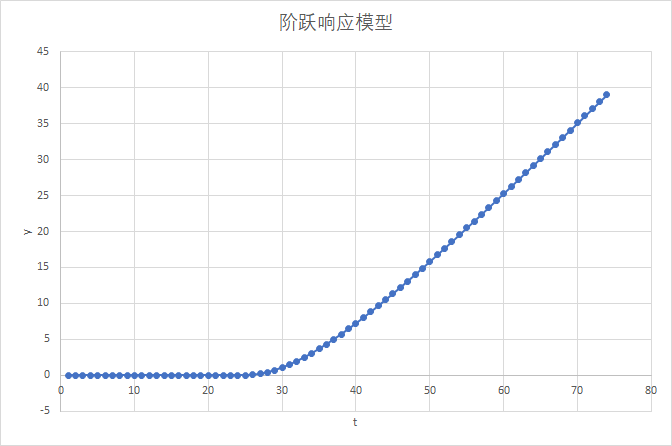
但是在MPC的模型配置中，需要输入的是该模型的差分模型，即下图。

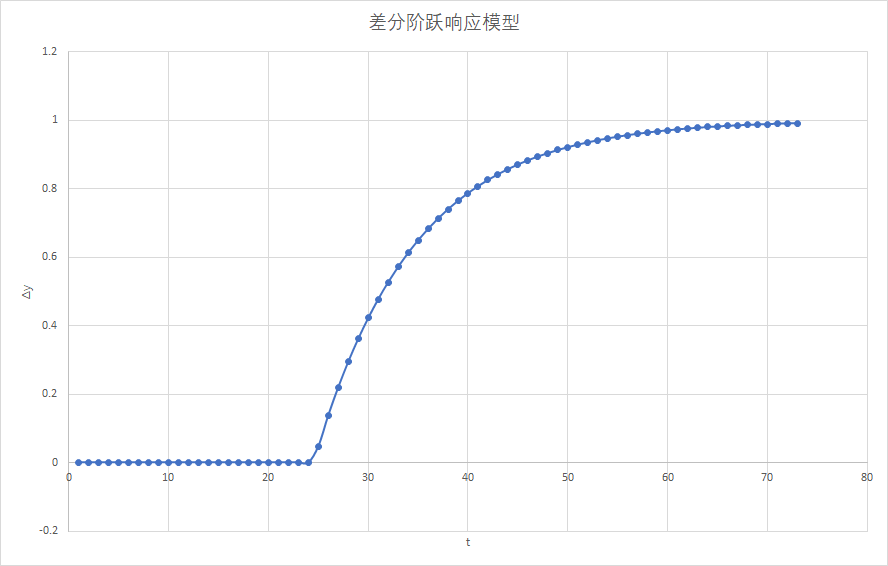
需要注意差分模型的FIR曲线和采样周期（即AICS的画布周期）有关，如果采样周期不同，差分模型的曲线也会不同。上图为采样周期为1秒的时候的差分模型曲线。如果采样周期为5秒，则对应的差分模型FIR曲线为：

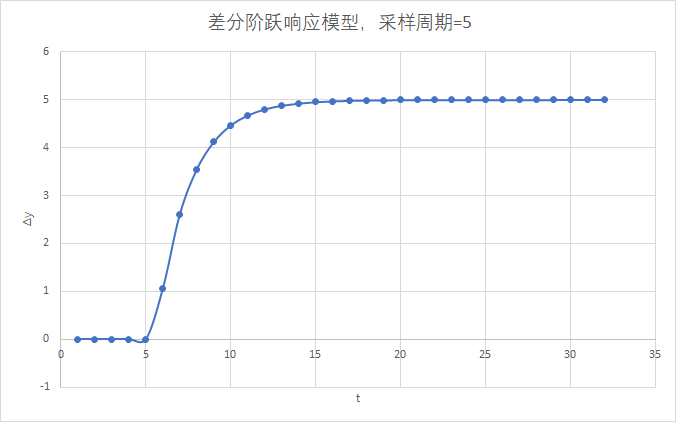
上图的采样周期为5秒，所以在原阶跃模型中，相邻两个采样点的距离变长，两个点的差也相应变大，造成了在采样周期为5秒的情况下，差分阶跃响应模型的增益为5。

• CV配置

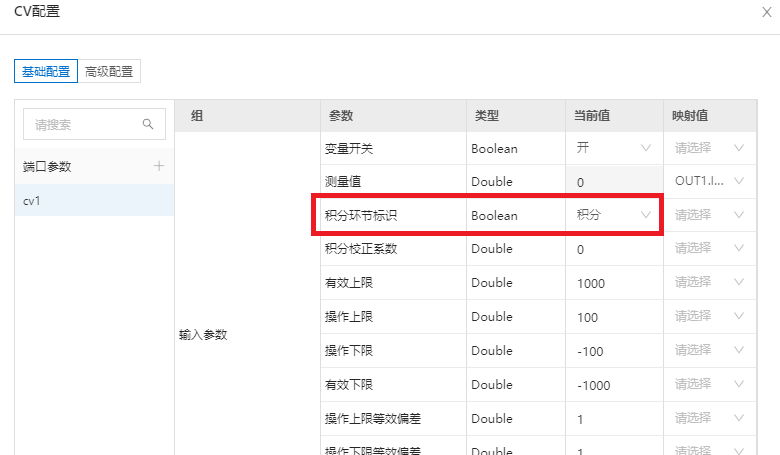
在积分环节控制器的CV配置中，需要将该CV的积分标识选为“积分”。

控制效果展示

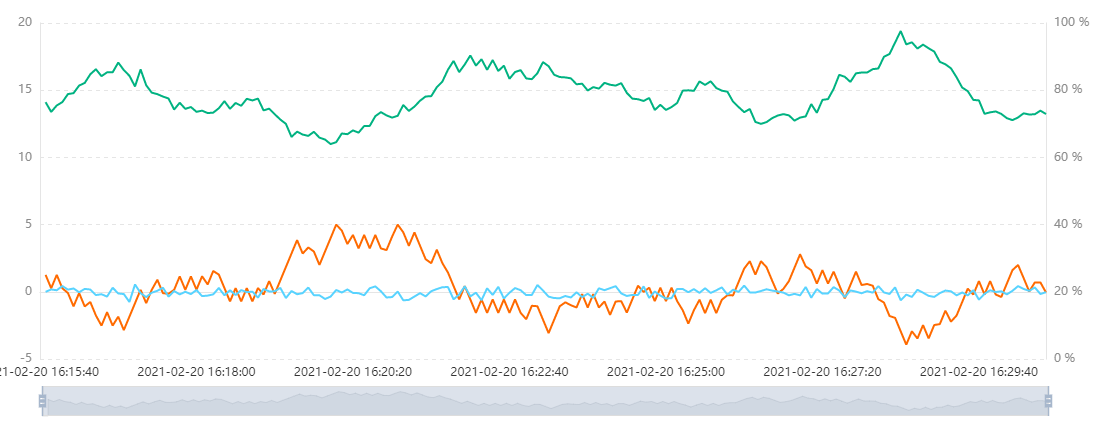
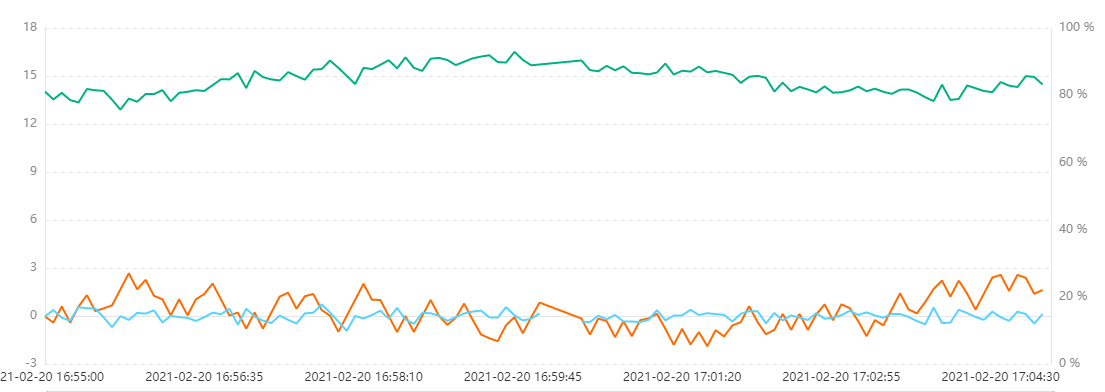
• 下游水箱液位测量值中加入白噪声

白噪声均值为0，标准差为0.3，下游水箱的液位设定值为15。图中所示绿线为下游水箱液位，红线为上游水箱入水口。

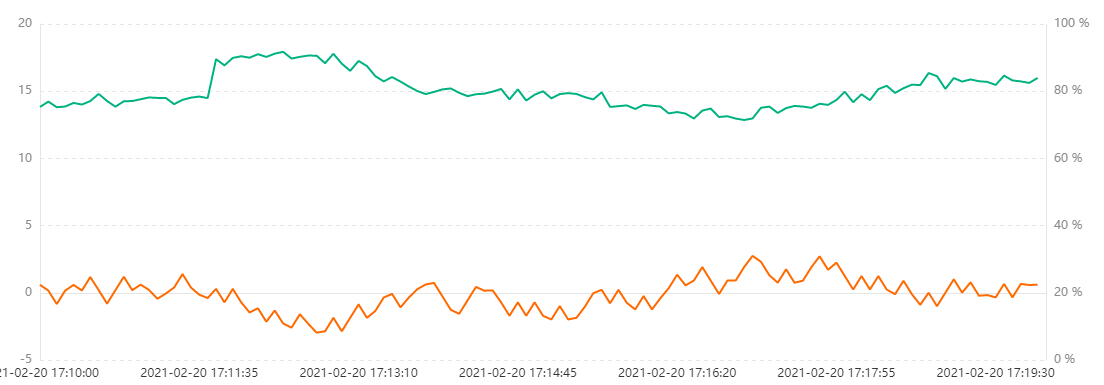
• 下游水箱第二入水口加入阶跃扰动

阶跃高度为3，均值为0标准差为0.3的白噪声依然存在，下游水箱液位设定值为15。

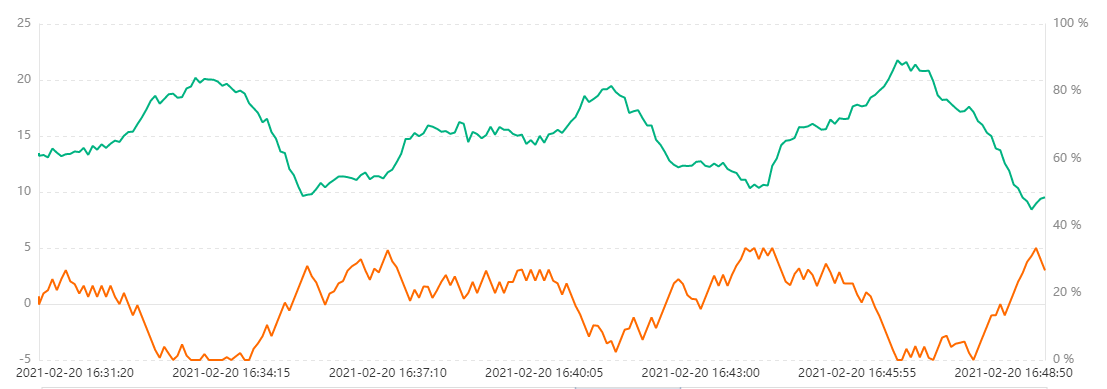
• 上游水箱第二入水口加入白噪声

上游水箱第二入睡就白噪声均值为0，标准差为0.05。下游水箱液位设定值为15。

控制器性能调优

如何解决积分CV变量的振荡现象，在此案例中，可以看到，当上游水箱的第二个入水口发生扰动的时候，控制器很难将下游水箱的液位控制在设定值附近。这是因为，上游水箱入水口的白噪声扰动通过上游水箱进入下游水箱之后，变成了一个有积分性质的噪声，这是只假设平移校正的MPC无法处理的。这类现象在积分环节的控制中非常常见，DT-MPC提供了一个解决方案，即积分校正系数。

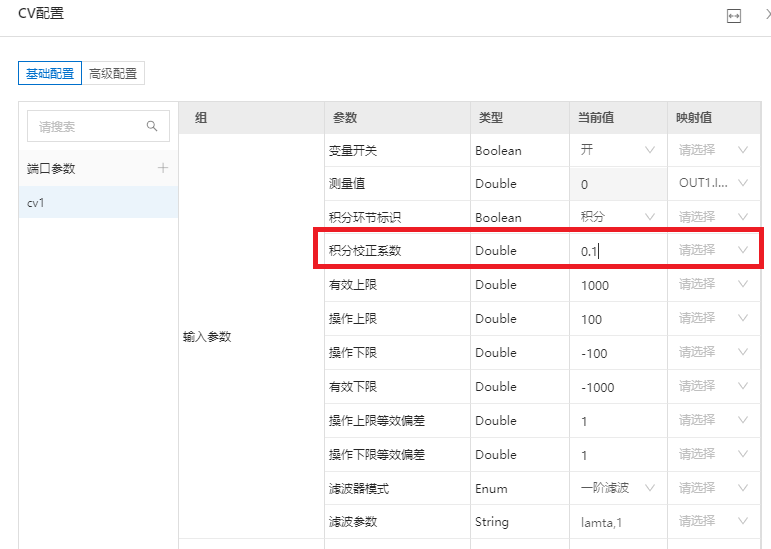
积分校正系数为积分环节控制特有的控制器参数。该系数的取值为[0,1]。该系数的大小决定了控制器在进行模型校正时，预测误差在绝对误差和速率误差上的分配。该系数为0时，误差校正将更偏向于绝对误差；反之，则更偏向于速率误差。在此案例中，上游水箱的扰动到达下游水箱时，变成了一个有积分性质的噪声，影响了下游水箱液位变化的速率。也就是说，我们需要将模型预测误差中的一部分认为是速率误差，即将积分校正系数设置成为一个大于0的数。考虑到速率误差，通常将积分校正系数设置在0.1~0.3的范围内。

在此案例中，我们将积分矫正误差设置为0.1，便可以清晰地看到控制效果的提升。