图算法

功能介绍

图计算服务GraphCompute新增图算法功能，基于当前服务的数据进行算法执行，方便用户快速进行全图数据的分析。只需要开通图计算服务实例，即可同时拥有高性能图数据的查询分析一体化引擎。相比业界方案，图计算服务方案更便捷，无需额外自运维数据链路，让数据流转更高效。

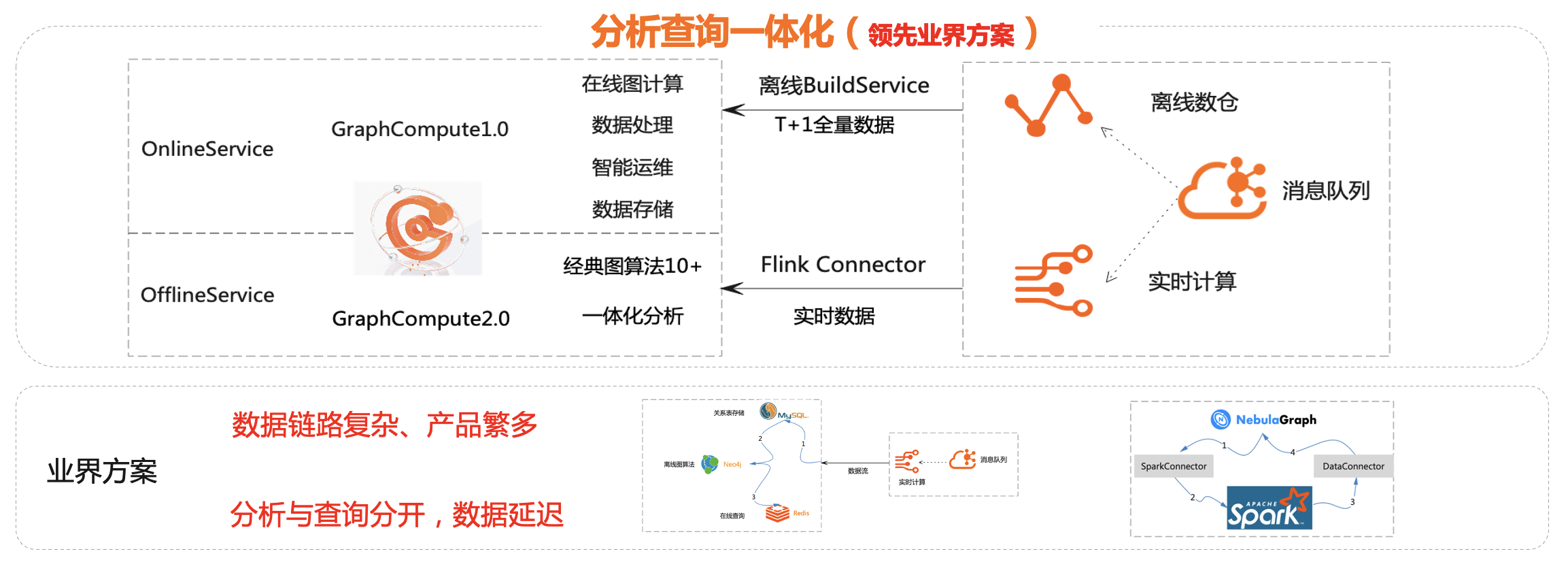
本期重点开放3个核心图算法，其他经典图算法持续开放中。

算法介绍

1）中心性算法 PageRank

PageRank算法是计算网页排名的经典算法。输入是一个有向图G，其中顶点表示网页。如果存在网页A到网页B的链接，则存在连接A到B的边。

算法的基本原理如下：

• 初始化：点值表示PageRank的rank值（DOUBLE类型）。初始时，所有点取值为1/TotalNumVertices。

• 迭代公式：PageRank(i)=0.15/TotalNumVertices+0.85*sum。其中sum为所有指向i点的点（设为j）PageRank(j)/out_degree(j)的累加值。

2) 社区发现 Weakly Connected Components

弱连通分量（WCC）算法在有向图和无向图中寻找连通节点集。如果两个节点之间存在路径，则表示两个节点已连接。相互连接的所有节点的集合形成一个组件。与强连接组件（SCC）相反，不考虑两个节点之间路径上的关系方向。例如，在有向图（a）→（b）中，即使没有向关系（b）→（a）， a和b也会在同一个分量中。

本算法计算每个点的连通分量成员，最后输出顶点值中包含最小顶点ID的连通分量。将最小顶点ID沿着边传播到连通分量的所有顶点。

3）路径查找 Single Source Shortest Path(Unweighted、Weighted)

单源最短距离是指给定图中一个源点，计算源点到其它所有节点的最短距离。Dijkstra算法是求解有向图中单源最短距离SSSP（Single Source Shortest Path）的经典算法。

Dijkstra算法是通过点去更新最短距离值，每个点维护到源点的当前最短距离值，当这个值发生变化时，将新值加上边的权值，发送消息通知其邻接点。下一轮迭代时，邻接点根据收到的消息，更新其当前最短距离值，当所有点的当前最短距离值不再变化时，迭代结束。

• 初始化：源点s到s自身的距离为0（d[s]=0），其他点u到s的距离为无穷（d[u]=∞）。

• 迭代：如果存在一条从u到v的边，则从s到v的最短距离更新为d[v]=min(d[v], d[u]+weight(u, v))，直到所有的点到s的距离不再发生变化时，迭代结束。

操作指南

准备工作

在进行全图分析之前，我们需要新建图计算实例和创建图配置，并完成图数据的批量导入或者API数据写入。

1）创建图计算服务实例，点击链接进行实例开通，早期测试阶段可选用【独享分析型】规格进行功能验证。

2）创建图配置，可参考最佳实践基于GraphCompute快速搭建好友推荐图应用进行业务数据和配置接入。

图算法配置

准备工作完成后可进行图算法任务配置，下面将基于好友关系的源数据进行最短路径、联通子图、PageRank三个算法的验证和配置解释。进入【实例详情】-【图算法】-【算法分析】页面新建和编辑算法配置，如需周期调度任务，可通过定时配置进行按天调度。

1）最短路径

确定边集选择，选中图中已关闭【索引优化】的边表可进行算法分析。支持选择多条边，对于部分可以用到边的权重字段的算法，可以选择边的权重字段，比如单源最短距离时可以用边的score字段表示边的长度，如果不选择权重字段，则边的长度默认为1

单源最短距离，需要填写的扩展参数为sourceIdLabel和sourceIdValue，分别表示算法需要的启动初始点的表中的字段名和对应的值。

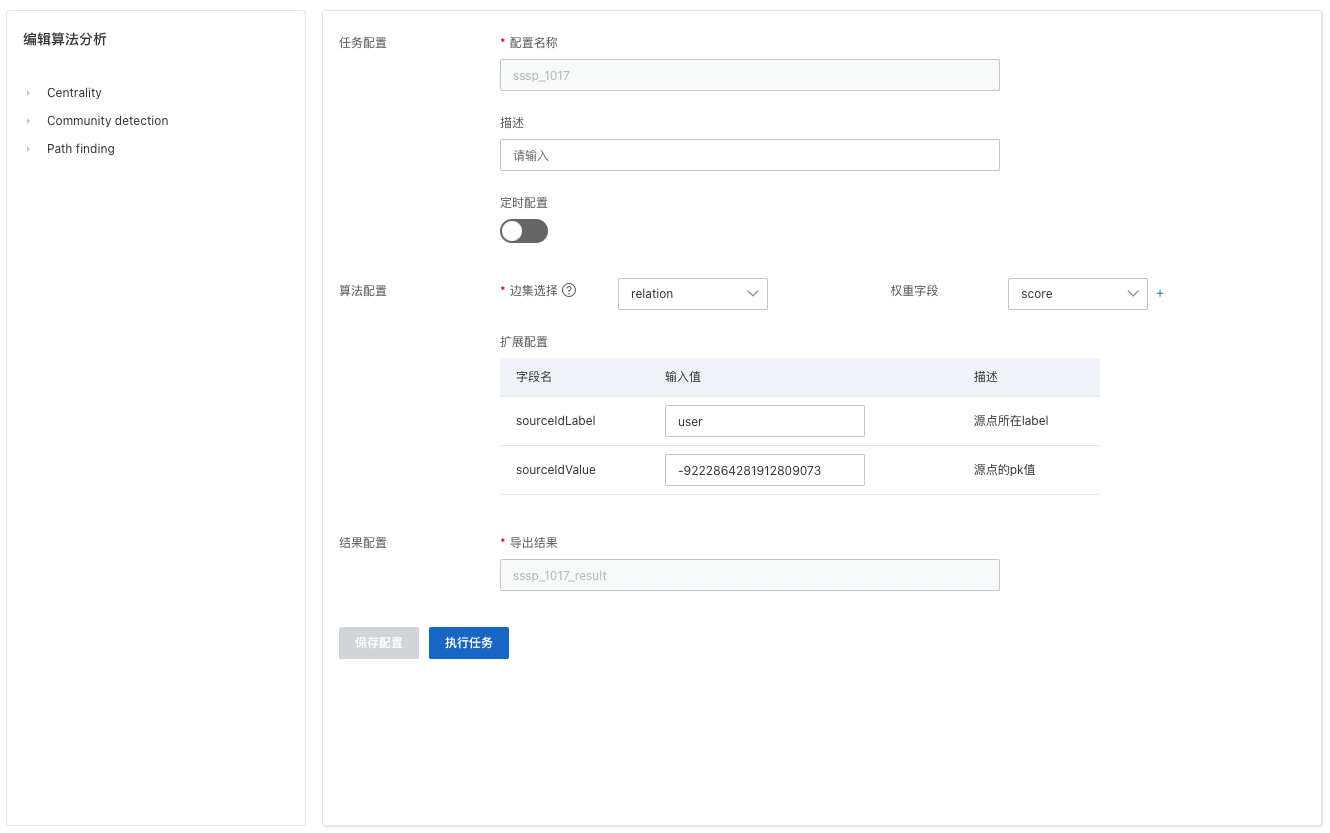
2）联通子图

只需要进行边集选择，选中图中已关闭【索引优化】的边表可进行算法分析；无需额外配置权重字段。

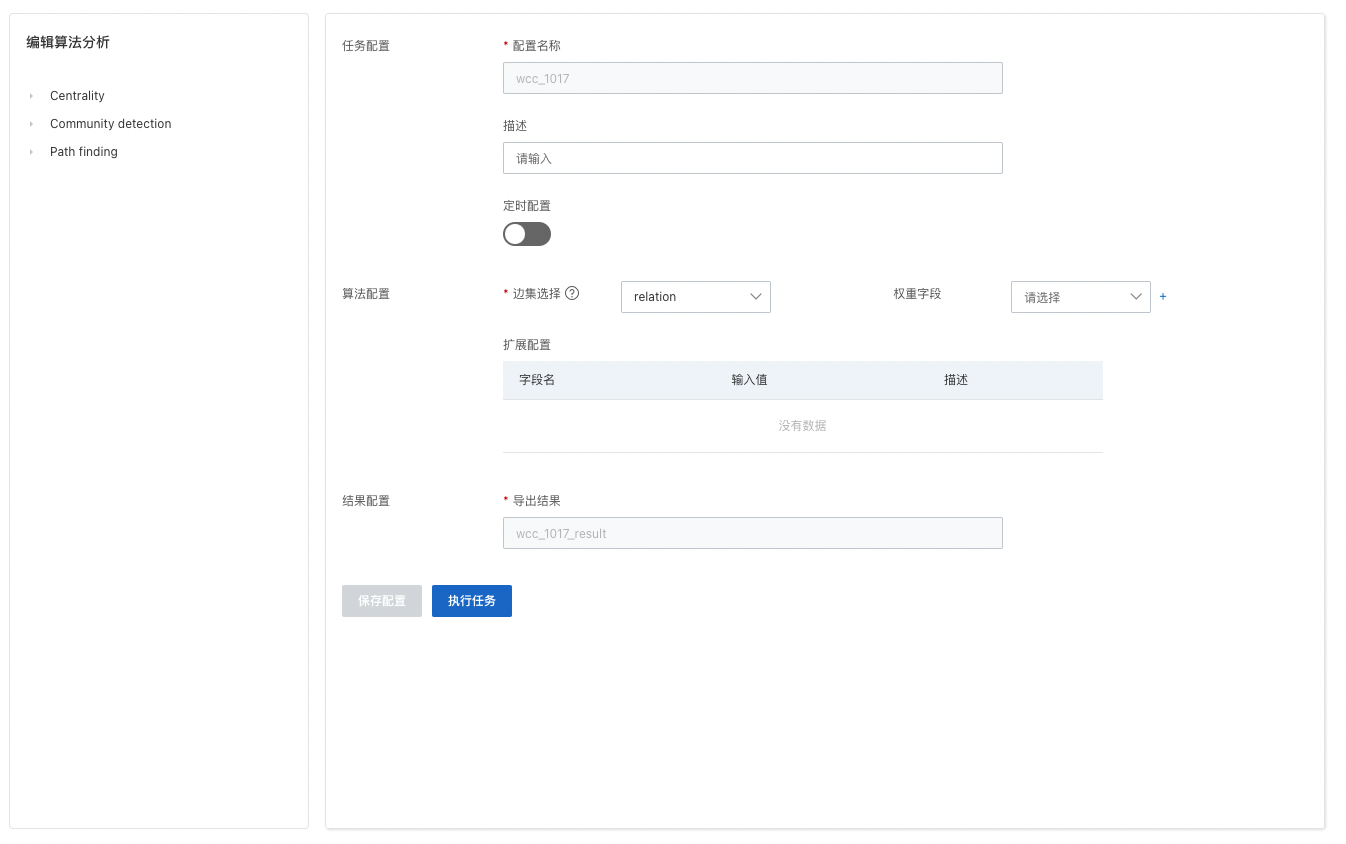
3）PageRank

确定边集选择，选中图中已关闭【索引优化】的边表可进行算法分析；

PageRank算法，需要填写的扩展参数为maxIteration，表示PageRank算法的最大迭代轮数

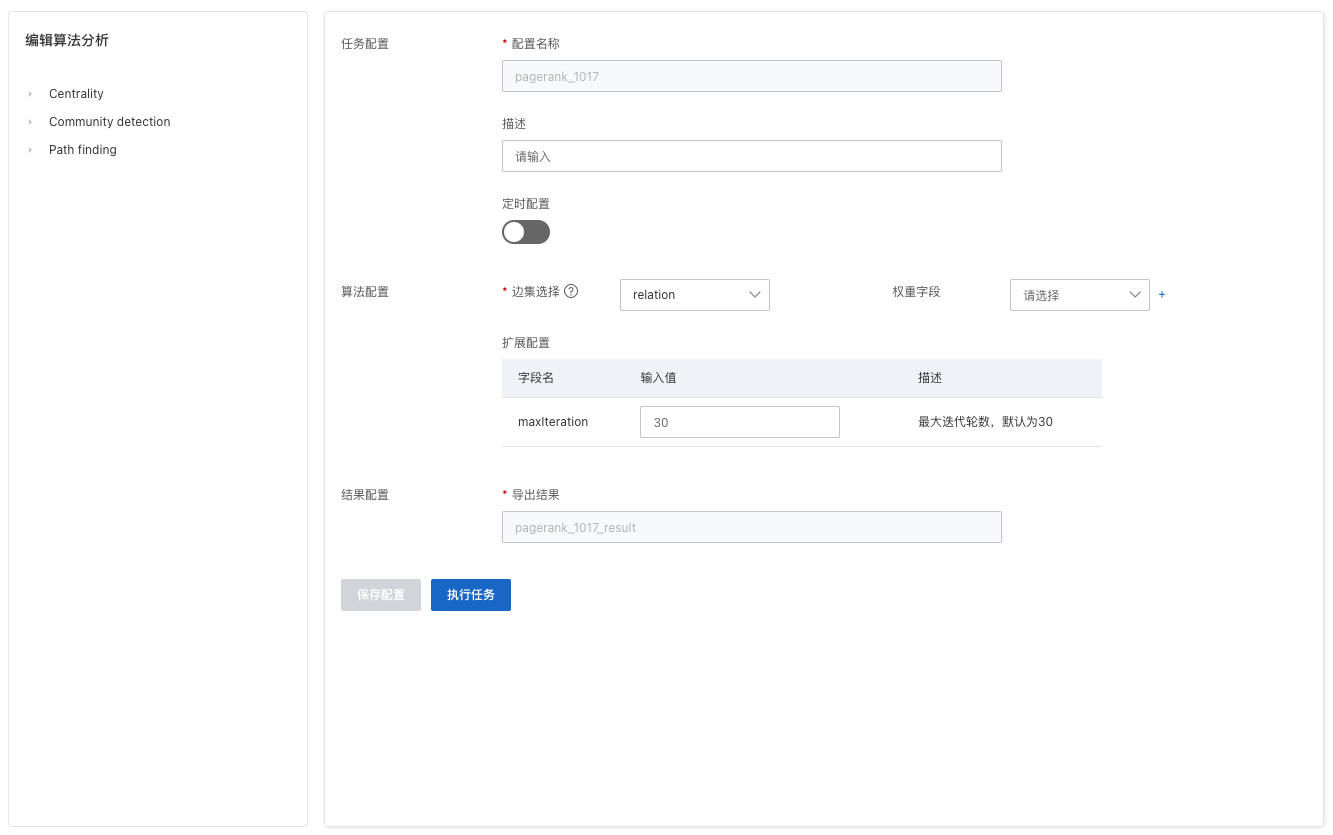
4）任务运行

点击图算法配置的"运行"按钮，弹窗提示计费之后点击确认即可运行，任务运行记录可以点击配置的“历史任务“进行查看；当前产品功能属于公测期间，暂不额外收费。

5）结果产出

点击“保存配置”成功创建图算法配置之后，会在图中自动创建出一个新的点，点的名称为填写的表格最下方的导出结果，后续运行图算法任务成功之后，任务结果会自动回流到该结果点，回流完成之后即可在线查询

查询分析结果

1）最短路径

该算法结果点为KV类型，distance字段表示源点到该点的最短距离，当该值为Long.MaxValue(2^63-1)时表示不存在源点到该点之间的路径，可根据ID查询点：g("user_relation_graph").V("user#-9222864281912809073").hasLabel("sssp_1011_new_result")

2）联通子图

该算法结果点为倒排类型，componentId字段表示联通子图ID：

可根据ID查询点：g("user_relation_graph").V("user#-1328036738095129493").hasLabel("填写结果配置的表名")

使用倒排查询的语法查询指定componentId下面的所有点：g("user_relation_graph").V().hasLabel("填写结果配置的表名").indexQuery("{\"match\":{\"component_id\":\"user#-1000713713241257875\"}}")

3）PageRank

该算法对应的结果点为KV类型，score字段表示pagerank分数，可根据ID查询点：g("user_relation_graph").V("user#-9222864281912809073").hasLabel("填写结果配置的表名")

应用场景

1）PageRank – 提高搜索覆盖率

诉求：搜索是服务平台中重要的一环，通过深化服务搜索能力，让用户可以直接搜索到服务内部的子服务，实现功能直达；在提升搜索整体体验的同时也为各行业带来更多转化价值。

问题：长尾关键词搜索结果少或无结果，纯文本匹配无结果。

方案：升级为图算法PageRank，引入更丰富的item信息和用户点击行为等信息，提升召回的多样性。

效果：全局搜索PVCTR提升2%以上（推荐结果点击数/推荐结果曝光数），全局搜索无结果率累计下降20%以上。

2）Weakly Connected Components - 账号融合

诉求：同一个人可能会注册多个电商账号，通过非正常手段获取利益。

方案：使用预设的规则建立账号间的强联系，比如使用同一个电话的账号极大可能属于同一个人

算法：强\弱连通分量算法

成效：取代原先的GraphX、spark系统，时间效率可提升10倍以上

扩展：实体合并（挖掘或识别利益共同体、同一对象），如同名户、集团客户等等，都可进行聚合。

计费规则

当前图算法功能处于公测期，可免费使用。后续正式上线后将根据数据量级进行资源评估，按照算法消耗的资源情况进行按量计费。