人员排班-任务分配(混合整数规划)_优化求解器(Optimization Solver)-阿里云帮助中心

行业背景

随着现在产业的发展，许多行业有不同时段的服务需要，人员排班的问题，逐渐成为了企业管理中的重要环节。如何合理、高效地进行人员排班，以帮助企业和机构提高管理效率、降低成本，同时提升员工的工作满意度和整体效能。这个优化问题也可以运用数学规划的方法来建模和求解。

例如：某企业对客服岗位进行排班，不同时间段有不同的用户需求。需要考虑每天的用工需求，以及一些排班规则和约束，尽量使排班的总班次最少，也就是人工成本最小化。

业务调研、数据量化、数学建模

在使用优化技术的时候，需要更详细的调研业务的需求，整理相关的业务逻辑和数据，并量化表示它。然后采用数学规划的方法进行数学建模。

此部分细节较多，可在案例人员排班中查阅细节，此处我们仅列出数学公式如下，参数部分请点击案例链接查看：

其中代表日期，代表班次，代表员工的上班状态，0代表没有值班，1代表值班。

以上公式对应的约束有：

每天各个班次在岗的人数符合需求
每人每天最多只有一个班次
前一天是晚班的，第二天不能是早班
一周工作的时间不能超过5天

源代码

MindOpt支持多种编程语言或者建模语言来调用。此处仅列出一种供参考：

MindOpt APL建模语言调用

此案例建模方法采用读取数据表格的方式，表格数据见人员排班案例。 MindOpt APL建模语言的源代码（可在人员排班线上试运行）：

##====MindOpt APL 建模语言版本代码====

clear model;

# 建模
# staffSchedule.mapl

set Schedule = {read "班次.csv" as "<1s>" skip 1}; # 读取班次的名称

set Day = {read "需求人数.csv" as "<1n>" skip 1}; #读取排班的日期
param maxDay = max(Day);
print "总共需要排班的天数为",maxDay;

param NumDemand = read "需求人数-长列表.csv" as "<1n,2s> 3n" skip 1; #读取每天各个班次的需求人数，原横纵表拉成长列表为了读取数据方便

param totalSlots = sum {<d,s> in Day*Schedule} NumDemand[d,s];
print "总共的待排班次数为",totalSlots;

#预估上班人数
param maxEmployee = ceil(totalSlots/5) + 1; #如果班次需求特殊导致不可解的时候，可以增加员工
print "设置参与排班人数：",maxEmployee;
set Employee = {1..maxEmployee};

#声明变量 
var x[Day*Schedule*Employee] binary; 

#约束
subto constraint_0 :
    forall {<d,s> in Day*Schedule}
         sum {e in Employee} x[d,s,e] >= NumDemand[d,s]; #满足用工需求

subto constraint_1 : 
    forall {<d,e> in Day*Employee}
            sum {s in Schedule} x[d,s,e] <= 1;  #每人每天只排一个班次
            
set DayPre = Day without {<maxDay>}; #去掉最后一天
subto constraint_2 : 
    forall {e in Employee}
        forall {d in DayPre}
            x[d,"夜班0-8点",e] + x[d+1,"早班8-16点",e] <= 1; #前一天晚班的，第二天不排早班

subto constraint_3 : 
    forall {e in Employee}
        sum {<d,s> in Day*Schedule} x[d,s,e] <= 5; #待排的7天里只上5天班
        
        
minimize minOnduty: sum {<d,s,e> in Day*Schedule*Employee} x[d,s,e];


#求解
option solver mindopt;     # （可选）指定求解用的求解器，默认是MindOpt
option mindopt_options 'print=0'; #设置求解器输出级别，减少过程打印
solve;         # 求解

# 结果打印和检查结果
print "-----------------Display---------------";
#display; #打印太多，注释了

param ondutySlots = sum {<d,s,e> in Day*Schedule*Employee} x[d,s,e];
print "有排班的班次总数：",ondutySlots;

结果和结果用法

不同代码日志打印不一样。部分结果日志打印如下所示：

待排7天的班
总共有99个班次待排
设置参与排班人数：21
Running mindoptampl
wantsol=1
print=0
MindOpt Version 1.0.0 (Build date: 20231013)
Copyright (c) 2020-2023 Alibaba Cloud.

Start license validation (current time : 13-NOV-2023 14:37:44).
License validation terminated. Time : 0.007s


OPTIMAL; objective 99.00

目标的最优解是：99。更多解的细节，如决策变量的取值、验证约束是否正确，可以通过print命令打印来显示，变量的取值也可以从程序运行写的.sol文件里面获取，还可以调用display获取所有变量的。

如运行如下指令，验证“一周工作时间不能超过5天”这个约束：

forall {e in Employee }
 print '员工{}安排了{}个班次'%e, sum{<d,s> in Day*Schedule} x[d,s,e];

输出结果是每个员工的工作天数最多五天：

员工1安排了5个班次
员工2安排了5个班次
员工3安排了4个班次
员工4安排了5个班次
员工5安排了5个班次
员工6安排了5个班次
员工7排了5个班次
员工8安排了5个班次
员工9安排了4个班次
员工10安排了5个班次
员工11安排了5个班次
员工12安排了5个班次
员工13安排了4个班次
员工14安排了3个班次
员工15安排了5个班次
员工16安排了5个班次
员工17安排了5个班次
员工18安排了5个班次
员工19安排了5个班次
员工20安排了4个班次
员工21安排了5个班次

运行如下代码，将输出打印为csv格式，作为人员排班问题的解决方案：

print "{}, {}, {}" % "日期", "班次", "员工" : "Schedule_Results.csv";
close "Schedule_Results.csv";

forall {<d,s,e> in Day*Schedule*Employee with x[d,s,e] >0}
    print "{}, {}, {}" % d, s,e >> "Schedule_Results.csv";

close "Schedule_Results.csv";

部分结果如下：

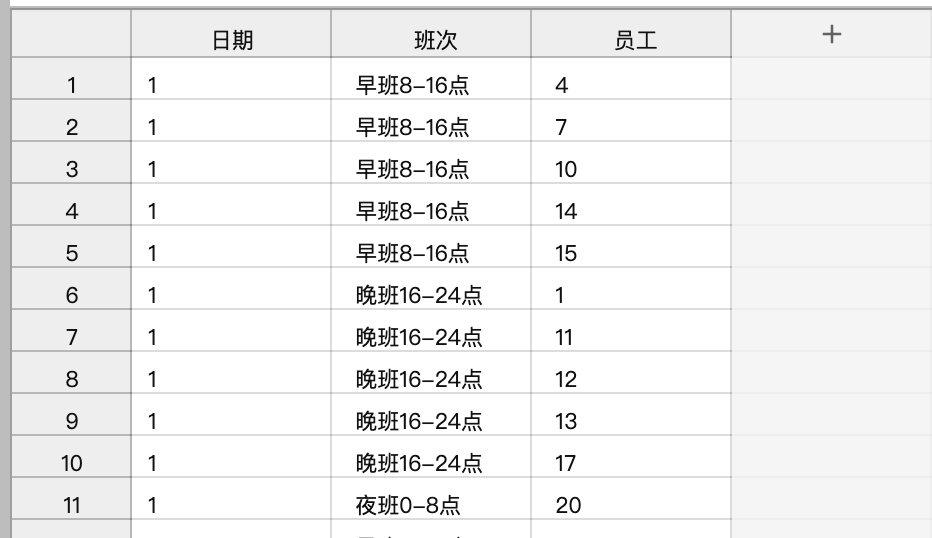
即，1号早班安排了编号4、7、10、14、15员工上早班。