交通调度-网络流最大流问题_优化求解器(Optimization Solver)-阿里云帮助中心

行业背景

交通调度是指对交通资源进行合理的调度和管理，以实现交通系统的高效运行和流量控制。如何安排调度，以帮助提高交通运输的效率，降低成本。这个优化问题也可以运用数学规划的方法来建模和求解。

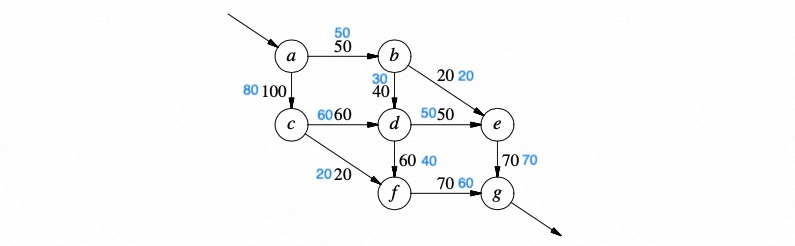
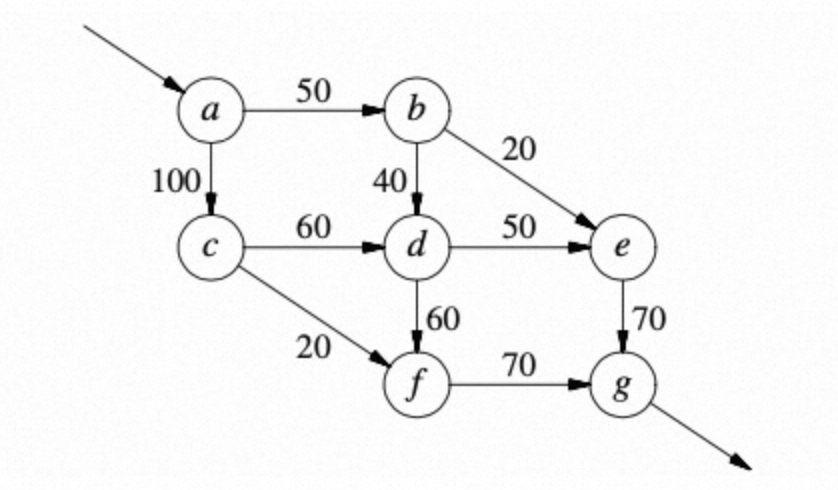
例如：已知有七个站点，每个站点都有若干条进站道路与出站道路，道路旁的数字表示单位时间内此路所能承载的最大车辆数，如何分配车辆使得单位时间从a站点出发，最后到达g站点的车辆最多？

业务调研、数据量化、数学建模

在使用优化技术的时候，需要更详细的调研业务的需求，整理相关的业务逻辑和数据，并量化表示它。然后采用数学规划的方法进行数学建模。

此部分细节较多，可在案例交通调度中查阅细节，此处我们仅列出数学公式如下，参数部分请点击案例链接查看：

其中i代表每段通道的起点，j代表通道的抵达点，e代表车辆的初始点，k代表每个中间的站点，r代表可以通过的车辆数

以上公式对应的约束有：

进入中间站点的车辆数等于该站点出去的车辆数
每条通道通过的车辆数有限制

源代码

MindOpt支持多种编程语言或者建模语言来调用。此处仅列出一种供参考：

MindOpt APL建模语言调用

MindOpt APL建模语言的源代码（可在交通调度上试运行）：

##====MindOpt APL 建模语言版本代码====

clear model;

# 建模
# net1.mapl
set Station :={"a","b","c","d","e","f","g"};
set Middle := {"b","c","d","e","f"};
set Roads :={<"a","b">,<"b","d">,<"c","d">,<"d","e">,<"e","g">,<"a","c">,<"b","e">,<"c","f">,<"d","f">,<"f","g">};

param entr := "a";

param lb := 0;
param ub[Roads] := <"a","b"> 50, <"b","d"> 40, <"c","d"> 60, <"d","e"> 50, <"e","g"> 70, <"a","c"> 100, <"b","e"> 20, <"c","f"> 20, <"d","f"> 60, <"f","g"> 70;

var x[<i,j> in Roads] >= lb <= ub[i,j];

maximize Total : sum {<entr,j> in Roads } x[entr,j]; #起点进入的最大流量

#流量均衡
subto Balance: 
    forall <k> in Middle do
        sum {<i,k> in Roads} x[i,k] == sum {<k,j> in Roads } x[k,j]; 


print "-----------------用MindOpt求解---------------";
option solver mindopt;     # （可选）指定求解用的求解器，默认是MindOpt
#option mindopt_options 'print=0'; #设置求解器输出级别，减少过程打印
solve;         # 求解

print "-----------------结果---------------";
display;        # 展示结果
print "经过优化后，最大流量=" ,sum {<entr,j> in Roads } x[entr,j];

结果和结果用法

不同代码日志打印不一样。部分结果日志打印如下所示：

...
Model summary.
 - Num. variables     : 10
 - Num. constraints   : 5
 - Num. nonzeros      : 16
 - Bound range        : [2.0e+01,1.0e+02]
 - Objective range    : [1.0e+00,1.0e+00]
 - Matrix range       : [1.0e+00,1.0e+00]
...
Simplex method terminated. Time : 0.002s


OPTIMAL; objective 130.00
...
-----------------结果---------------
经过优化后，最大流量=130

目标的最优解是：130。更多解的细节，如决策变量的取值、验证约束是否正确，可以通过print命令打印来显示，变量的取值也可以从程序运行写的.sol文件里面获取，还可以调用display获取所有变量的。

如运行如下指令，验证“进入中间站点的车辆数等于该站点出去的车辆数”这个约束：

forall <k> in Middle do
  print '进入{}站点的车辆数:{}'%k, sum {<i,k> in Roads} x[i,k];
print "-------------";
forall <k> in Middle do
  print '离开{}站点的车辆数:{}'%k, sum {<k,j> in Roads} x[k,j];

输出结果是对等的：

进入b站点的车辆数:50
进入c站点的车辆数:80
进入d站点的车辆数:90
进入e站点的车辆数:70
进入f站点的车辆数:60
-------------
离开b站点的车辆数:50
离开c站点的车辆数:80
离开d站点的车辆数:90
离开e站点的车辆数:70
离开f站点的车辆数:60

运行如下代码，将输出打印为csv格式，作为交通调度问题的解决方案：

print "{},{},{} "% "起点","途径点","车辆数" : "Results.csv";
close "Results.csv";

forall {<i,j> in Roads}
    print "{},{},{}" % i,j,x[i,j]  >> "Results.csv";

close "Results.csv";

输出结果如下：

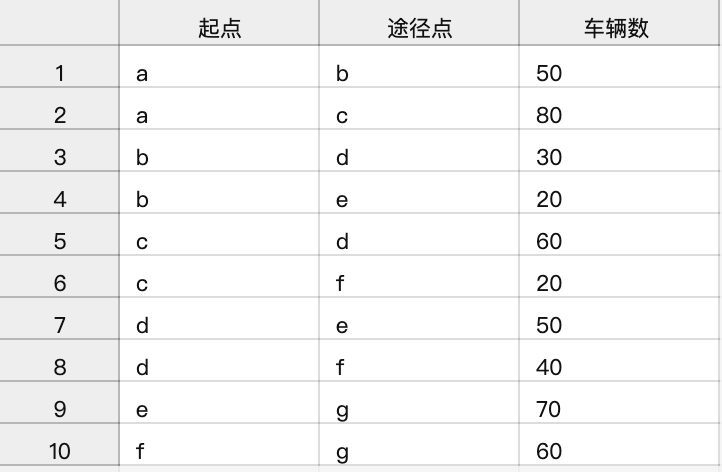
即，从a站最多可出发130辆车。并且分流的流量为，如下图

a到b是50，到c是80；
- b到d是30，到e是20
- c到d是60，到f是20
  - d汇总了90的流量，分流到e是50，到f是40
    - e汇总了70的流量
    - f汇总了60的流量 -它们都汇总到出口g，总共是130