相关性函数

相关性算子

• 只支持华东2（上海）地域。

• 相关性算子支持最大数据量为1000万行。

• 用于离线调度的相关性算子。

• 计算两组数据的相关系数r。两组数据之间的相关程度通过相关系数r来表示。相关系数r的取值范围是-1～1。两组数据正相关时，r值在0～1范围；两组数据负相关时，r值在-1～0范围。

函数格式

SELECT correlation_analysis_pair(Col_1,Col_2,method)

输入参数

• method：必填。JSON类型。

  • 'pearson'：皮尔森相关（Pearson），适用于变量是连续型变量（又称等间隔测度变量）。

  • 'spearman'：斯皮尔曼相关（Spearman）：适合于有序变量或不满足正态分布假设的等间隔数据。

  • 'kendall'：肯德尔相关（Kendall），适合于有序变量或不满足正态分布假设的等间隔数据。

• Col_1：必选。double或int类型。分析的目标列。

• Col_2：必选。double或int类型。被观测的指标列

输出参数

• string：string类型。输出格式[r,p]。

  • r是相关性系数, double或int类型，范围是-1～1。r的绝对值越接近1，两组数据的相关性越强。

  • p是假设检验的显著性值, double或int类型。

  • 假设检验分为假设和检验，首先假定原假设为真，然后通过样本数据检验原假设是否成立。

    1. 确定原假设和备择假设。原假设是两组数据没有相关性，备择假设是两组数据有相关性。

    2. 确定显著性水平。显著性水平代表了，原假设为真的情况下，拒绝原假设的概率。在实践中一般选显著性水平为0.05。

    3. 计算p值。p值代表在原假设成立的情况下，计算得到的相关系数或绝对值更大的相关性系数出现的概率。

    4. 当概率p小于显著性水平0.05时，这个概率非常小，意味着样本数据或更极端数据的出现是不可能事件。因此我们有足够的理由拒绝原假设，认为这两组数据存在相关性。当p大于等于显著性水平0.05时，我们接受原假设，认为这两组数据不存在相关性。

函数示例一

-- 示例1:
SELECT  correlation_analysis_pair(num1,num2,'spearman')
FROM  table
-- 示例2:
SELECT  correlation_analysis_pair(num1,num2,method)
FROM    VALUES
        (0.3,1,'pearson')
        ,(0.9,2,'pearson')
        ,(2.7,3,'pearson')
        ,(2,4,'pearson')
        ,(3.5,5,'pearson')
        ,(5,6,'pearson') t(num1,num2,method)
;

函数示例二

在物联网场景中，设备传感器会采集各种维度的数据，这些数据指标可能具有相关性。识别出数据指标间的相关性有助于探索分析数据的特征，也是后续建立模型的基础。

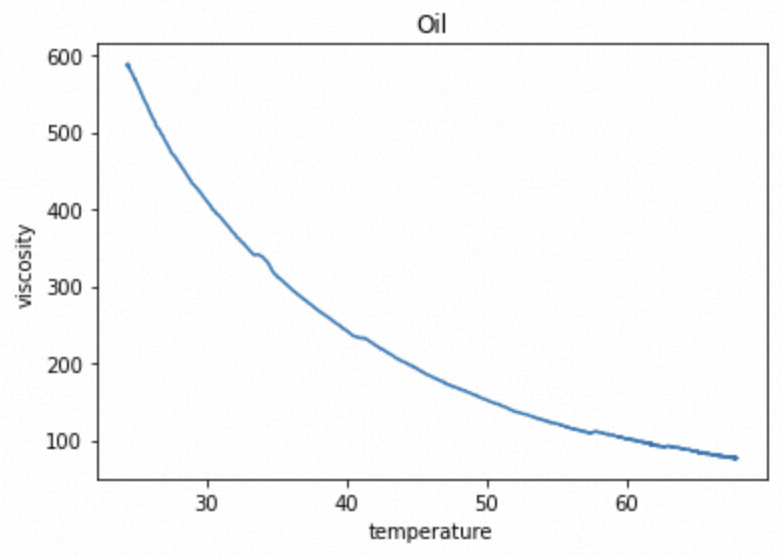
下载经过处理的油液温度和黏度数据。例如油液的温度和黏度具有高度相关性。在油液品质稳定时，油液的温度和黏度的变化趋势是相反的。因为温度和黏度均为连续数据，采用pearson方法。

SELECT  correlation_analysis_pair(num1,num2,'pearson')
FROM correlation_analysis_case_test;

输出[r,p]=[-0.94, 0.0]。r = -0.94说明温度和黏度数据明显负相关。p=0说明两组数据的相关性非常显著。下图为某种油液的温度-黏度示意图。