如何通过PASE插件实现高维向量检索(O引擎)_云原生数据库 PolarDB(PolarDB)-阿里云帮助中心

本文介绍PolarDB PostgreSQL版（兼容Oracle）如何通过PASE插件（基于IVFFlat或HNSW算法）实现高维向量检索。

背景信息

近年来，深度学习领域内的表示学习技术，作为人工智能的代表性技术，取得了长足性进展，在工业界中已经被大量应用，例如广告投放、人脸支付、图像识别、语音识别等场景。数据被嵌入至高维度向量，然后通过向量检索技术来查找相关的项目。

PASE（PostgreSQL ANN search extension）是一款为PostgreSQL数据库研发的高性能向量检索索引插件，使用业界中成熟稳定且高效的ANN（Approximate nearest neighbor）检索算法，包括IVFFlat和HNSW算法，通过这两种算法，可以在PG数据库中实现极高速向量查询。PASE暂时不支持特征向量的抽取与产出，您需要自己检索实体的特征向量，PASE负责的工作是根据已产出的海量级别的向量进行相似向量的检索。

目标读者

限于篇幅，本文不会对机器学习领域的相关名词做详细解释，所以阅读本文需要您有机器学习、搜索推荐相关知识基础。

注意事项

索引会有膨胀，大约的膨胀率可以通过select pg_relation_size('index名称');查询，当膨胀远大于数据的大小，并且查询有明显变慢时，需要重建索引。
数据频繁更新后索引会不精确，如果要求绝对准确，需要定期重建索引。
IVFFlat索引如果使用内部中心点（clustering_type=1），需要先在表中插入一定数据，再创建索引。
请使用高权限账号执行本文SQL示例。

使用限制

跨机并行查询仅支持顺序检索高维向量。

PASE算法简述

IVFFlat算法
IVFFlat是IVFADC的简化版本，适合于召回精度要求高，但对查询耗时要求不严格（100ms级别）的场景。相比其他算法，IVFFlat算法具有以下优点：
- 如果查询向量是候选数据集中的一员，那么IVFFlat可以达到100%的召回率。
- 算法简单，因此索引构建更快，存储空间更小。
- 聚类中心点可以由使用者指定，通过简单的参数调节就可以控制召回精度。
- 算法参数可解释性强，用户能够完全地控制算法的准确性。
IVFFlat的算法原理参见下图。
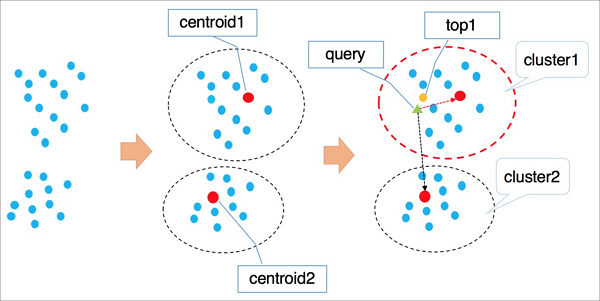
算法流程说明：
1. 高维空间中的点基于隐形的聚类属性，按照kmeans等聚类算法对向量进行聚类处理，使得每个类簇有一个中心点。
2. 检索向量时首先遍历计算所有类簇的中心点，找到与目标向量最近的n个类簇中心。
3. 遍历计算n个类簇中心所在聚类中的所有元素，经过全局排序得到距离最近的k个向量。
说明
- 在查询类簇中心点时，会自动排除远离的类簇，加速查询过程，但是无法保证最优的前k个向量全部在这n个类簇中，因此会有精度损失。您可以通过类簇个数n来控制IVFFlat算法的准确性，n值越大，算法精度越高，但计算量会越大。
- IVFFlat和IVFADC的第一阶段完全一样，主要区别是第二阶段计算。IVFADC通过积量化来避免遍历计算，但是会导致精度损失，而IVFFlat是暴力计算，避免精度损失，并且计算量可控。
HNSW算法
HNSW（Hierarchical Navigable Small World）算法适合超大规模的向量数据集（千万级别以上），并且对查询延时有严格要求（10ms级别）的场景。
HNSW基于近邻图的算法，通过在近邻图快速迭代查找得到可能的相近点。在大数据量的情况下，使用HNSW算法的性能提升相比其他算法更加明显，但邻居点的存储会占用一部分存储空间，同时召回精度达到一定水平后难以通过简单的参数控制来提升。
HNSW的算法原理参见下图。
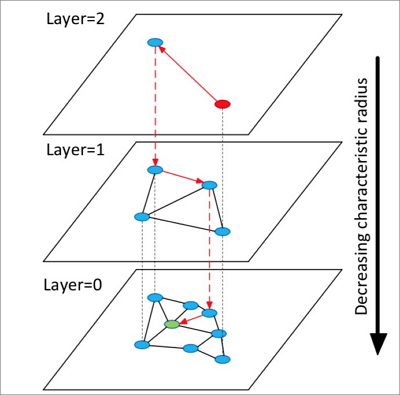
算法流程说明：
1. 构造多层图，每层图都是下层图的一个缩略，同时构成下层图的跳表，类似高速公路。
2. 从顶层随机选中一个点开始查询。
3. 第一次搜索其邻居点，把它们按距离目标的远近顺序存储在定长的动态列表中，以后每一次查找，依次取出动态列表中的点，搜索其邻居点，再把这些新探索的邻居点插入动态列表，每次插入动态列表需要重新排序，保留前k个。如果列表有变化则继续查找，不断迭代直至达到稳态，然后以动态列表中的第一个点作为下一层的入口点，进入下一层。
4. 循环执行第3步，直到进入最底层。
说明 HNSW算法是在NSW算法的单层构图的基础上构造多层图，在图中进行最近邻查找，可以实现比聚类算法更高的查询加速比。

两种算法都有特定的适用业务场景，例如IVFFlat适合高精图像对比场景，HNSW适合搜索推荐的召回场景。后续会陆续集成业界领先的算法实现到PASE中。

使用PASE

创建PASE插件。命令如下：
```
CREATE EXTENSION pase;
```
计算向量相似度。您可以通过以下两种构造方式计算向量相似度：
- 采用PASE数据类型构造方式计算
  示例
```
SELECT ARRAY[2, 1, 1]::float4[] <?> pase(ARRAY[3, 1, 1]::float4[]) AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> pase(ARRAY[3, 1, 1]::float4[], 0) AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> pase(ARRAY[3, 1, 1]::float4[], 0, 1) AS distance;
```
  说明
  - <?>是PASE类型的操作符，表示计算左右两个向量的相似度。左边向量数据类型必须为float4[]，右边向量数据类型必须为pase。
  - pase类型为插件内定义的数据类型，最多包括三个构造函数。以示例第三条的float4[], 0, 1部分进行说明：第一个参数为float4[]，代表右向量数据类型；第二个参数在此处没有特殊作用，可以填入0；第三个参数表示相似度计算方式，0表示欧氏距离，1表示点积（内积）。
  - 左右向量的维度必须相等，否则计算会报错。
- 采用字符串构造方式计算
  示例
```
SELECT ARRAY[2, 1, 1]::float4[] <?> '3,1,1'::pase AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> '3,1,1:0'::pase AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> '3,1,1:0:1'::pase AS distance;
```
  说明采用字符串构造方式和采用PASE数据类型构造方式都是计算两个向量相似度，区别是字符串构造方式通过英文冒号（:）分隔。以示例第三条的3,1,1:0:1部分进行说明：第一个参数表示右向量；第二个参数在此处没有特殊作用，可以填入0；第三个参数表示相似度计算方式，0表示欧氏距离，1表示点积（内积）。

创建索引。您可以使用两种算法创建索引：

说明对于要使用PASE向量索引的用户，如果采用欧氏距离作为向量相似度计算公式，原始向量不需要做任何处理，但如果采用内积或余弦作为向量相似度计算公式，需要对向量进行归一化处理，如原始向量为

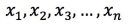，则需要满足：

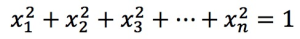，此时内积和余弦值相同。

IVFFlat算法创建索引

示例

CREATE INDEX ivfflat_idx ON vectors_table
USING
  pase_ivfflat(vector)
WITH
  (clustering_type = 1, distance_type = 0, dimension = 256, base64_encoded = 0, clustering_params = "10,100");

参数说明如下。


参数	说明
clustering_type	IVFFlat算法对向量数据进行的聚类操作类型。必填项。取值： 0：外部聚类，加载外部提供的中心点文件，由参数clustering_params控制。 1：内部聚类，即构建索引过程首先会在内部进行聚类操作，采用kmeans算法，由参数clustering_params控制。对于初级用户，建议使用内部聚类方式。
distance_type	相似度计算方式。默认值为0。取值： 0：欧式距离。 1：点积（内积）。使用此方式需要进行向量归一化，此时点积（内积）值的序和欧氏距离的序是反序关系。当前仅支持欧式距离，点积（内积）需要向量归一化后，采用附录中提供的方法计算。
dimension	向量维度。必填项，最大支持512。
base64_encoded	数据是否采用base64编码。默认为0。取值： 0：采用float4[]表示向量类型。 1：采用float[]的base64编码字符串表示向量类型。
clustering_params	对于外部聚类，该参数配置为中心点文件路径；对于内部聚类，该参数配置为聚类参数。格式为：`clustering_sample_ratio,k`。必填项。 clustering_sample_ratio：以1000为分母的聚类采样比例。取值范围为(0,1000]内的整数，例如值为1，表示对表中的数据按照千分之一的比例采样后进行kmeans聚类。值越大查询准确率越高，但创建索引的时间越长，建议采样的数据总量不要超过10万条。 k：聚类中心数，值越大查询准确率越高，但创建索引时间越长，建议取值范围为[100,1000]。

HNSW算法创建索引

示例

CREATE INDEX hnsw_idx ON vectors_table
USING
  pase_hnsw(vector)
WITH
  (dim = 256, base_nb_num = 16, ef_build = 40, ef_search = 200, base64_encoded = 0);

参数说明如下。


参数	说明
dim	向量维度。必填项，最大支持512。
base_nb_num	图中节点的邻居数。必填项。值越大查询准确率越高，但建索引时间越慢，同时索引量占空间越大，建议取值范围[16-128]。
ef_build	创建索引过程中的堆长度。必填项。越长效果越好，但创建索引越慢，建议取值范围[40,400]。
ef_search	查询过程中的堆长度。必填项。越长效果越好，但查询性能越差，可在查询时指定，该处为默认值：200。
base64_encoded	数据是否采用base64编码。默认值0。取值： 0：采用float4[]表示向量类型。 1：采用float[]的base64编码字符串表示向量类型。

查询。您可以使用两种索引查询：
- 使用IVFFlat索引查询
  示例
```
SELECT id, vector <#> '1,1,1'::pase as distance
FROM vectors_ivfflat
ORDER BY
vector <#> '1,1,1:10:0'::pase
ASC LIMIT 10;
```
  说明
  - <#>为IVFFlat算法索引的操作符。
  - 向量索引通过ORDER BY语句生效，支持ASC升序排序。
  - PASE数据类型为三段式，通过英文冒号（:）分隔。以示例的1,1,1:10:0进行说明：第一段为查询向量；第二段为IVFFlat的查询效果参数，取值范围为(0,1000]，值越大查询准确率越高，但查询性能越差，建议根据实际数据进行调试确定；第三段为查询时相似度计算方式，0表示欧式距离，1表示点积（内积）。使用点积（内积）方式需要进行向量归一化，此时点积（内积）值的序和欧氏距离的序是反序关系。
- 使用HNSW索引查询
  示例
```
SELECT id, vector <?> '1,1,1'::pase as distance
FROM vectors_ivfflat
ORDER BY
vector <?> '1,1,1:100:0'::pase
ASC LIMIT 10;
```
  说明
  - <?>为HNSW算法索引的操作符。
  - 向量索引通过ORDER BY语句生效，支持ASC升序排序。
  - PASE数据类型为三段式，通过英文冒号（:）分隔。以示例的1,1,1:10:0进行说明：第一段为查询向量；第二段为HNSW的查询效果参数，取值范围为（0,∞），值越大查询准确率越高，但查询性能越差，建议根据实际数据进行调试确定，初始值建议从40开始；第三段为查询时相似度计算方式，0表示欧式距离，1表示点积（内积）。使用点积（内积）方式需要进行向量归一化，此时点积（内积）值的序和欧氏距离的序是反序关系。

附录

点积（内积）方式计算示例

示例采用HNSW算法索引，创建FUNCTION示例如下：

CREATE OR REPLACE FUNCTION inner_product_search(query_vector text, ef integer, k integer, table_name text) RETURNS TABLE (id integer, uid text, distance float4) AS $$
BEGIN
    RETURN QUERY EXECUTE format('
    select a.id, a.vector <?> pase(ARRAY[%s], %s, 1) AS distance from 
    (SELECT id, vector FROM %s ORDER BY vector <?> pase(ARRAY[%s], %s, 0) ASC LIMIT %s) a
    ORDER BY distance DESC;', query_vector, ef,  table_name,  query_vector, ef, k);
END
$$
LANGUAGE plpgsql;

说明对于归一化的向量，内积=余弦，所以余弦值也可以用上述方式计算。

IVFFlat索引自定义中心点文件
此功能为高级功能，需要在服务器上指定路径上传中心点文件，并作为索引参数构建索引。详细参数请参见IVFFlat索引参数描述。文件格式如下：
```
向量维度|中心点个数|中心点向量集合
```
示例
```
3|2|1,1,1,2,2,2
```

高维向量检索（PASE）