本文为您介绍GMM聚类组件。
功能说明
GMM(Gaussian Mixture Model)是一个将事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型,混合高斯分布( MoG)由多个混合成分组成,每一个混合成分对应一个高斯分布。当聚类问题中各个类别的尺寸不同、聚类间有相关关系的时候,往往使用混合高斯分布更合适。
计算逻辑原理
高斯混合模型试图找到多维高斯模型概率分布的混合表示,从而拟合出任意形状的数据分布。
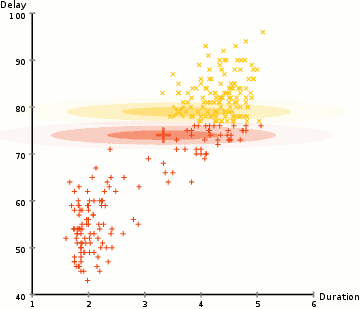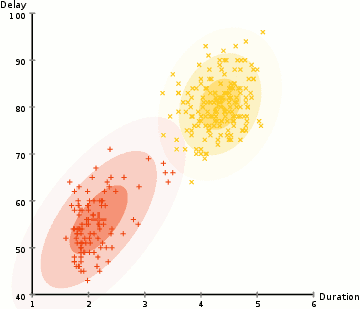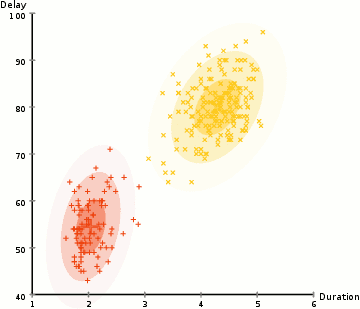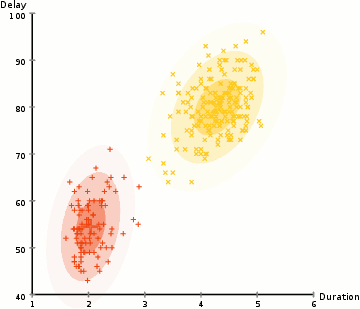
图:GMM聚类过程
参数说明
IN端口
参数名 | 参数描述 | 是否必填 | 输入数据类型 | 数据源类型 |
特征变量 | 配置模型特征变量。 | 是 | 整数或浮点数 说明 若存在非数值数据,则会抛出异常。 |
|
OUT端口
参数名 | 参数描述 | 输入数据类型 |
输出 | 聚类完成后输出具体的聚类类别“label”。 | 整型 |
算法参数
参数名 | 参数描述 | 是否必填 | 参数默认值 | 参数范围 |
混合成分数量 | 混合高斯模型个数。 | 是 | 2 | [2,99999999] |
协方差类型 |
| 是 | 完全协方差矩阵 |
|
EM 迭代停止阈值 | EM迭代停止阈值,当下限平均增益低于此阈值时,EM迭代将停止。 | 是 | 0.001 | [0,99999999] |
协方差对角非负正则化 | 协方差对角非负正则化,保证协方差矩阵均为正,非负正则化添加到协方差的对角线上。 | 是 | 0.000001 | [0,99999999] |
最大迭代次数 | 要执行的EM迭代次数。 | 是 | 100 | [1,99999999] |
初始化次数 | 要执行的初始化次数,用于产生最佳初始参数。 | 是 | 1 | [1,99999999] |
其他参数
参数名 | 参数描述 |
模型结果 | 模型结果展示模型聚类效果以及聚类结果,其中“CH分数(即Calinski-Harabasz指标)”和“轮廓系数”反应聚类效果,值越大,说明聚类效果越好。 |
